Behind the Plans

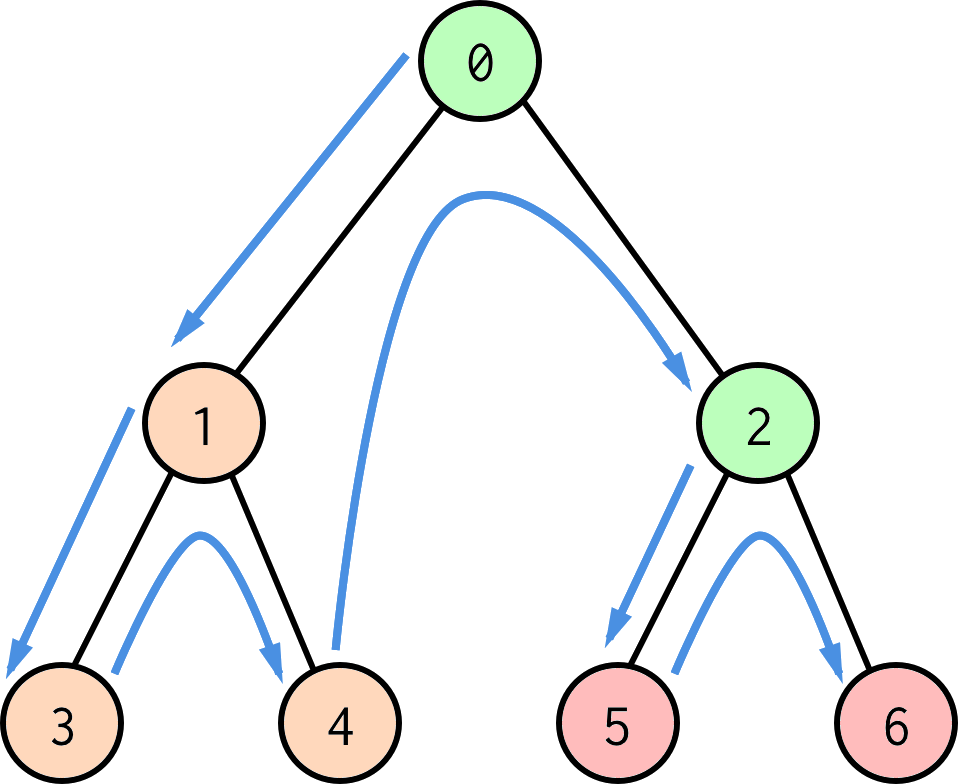
What defines a simulation? In Plans, every simulation is a tree structure like shown below:

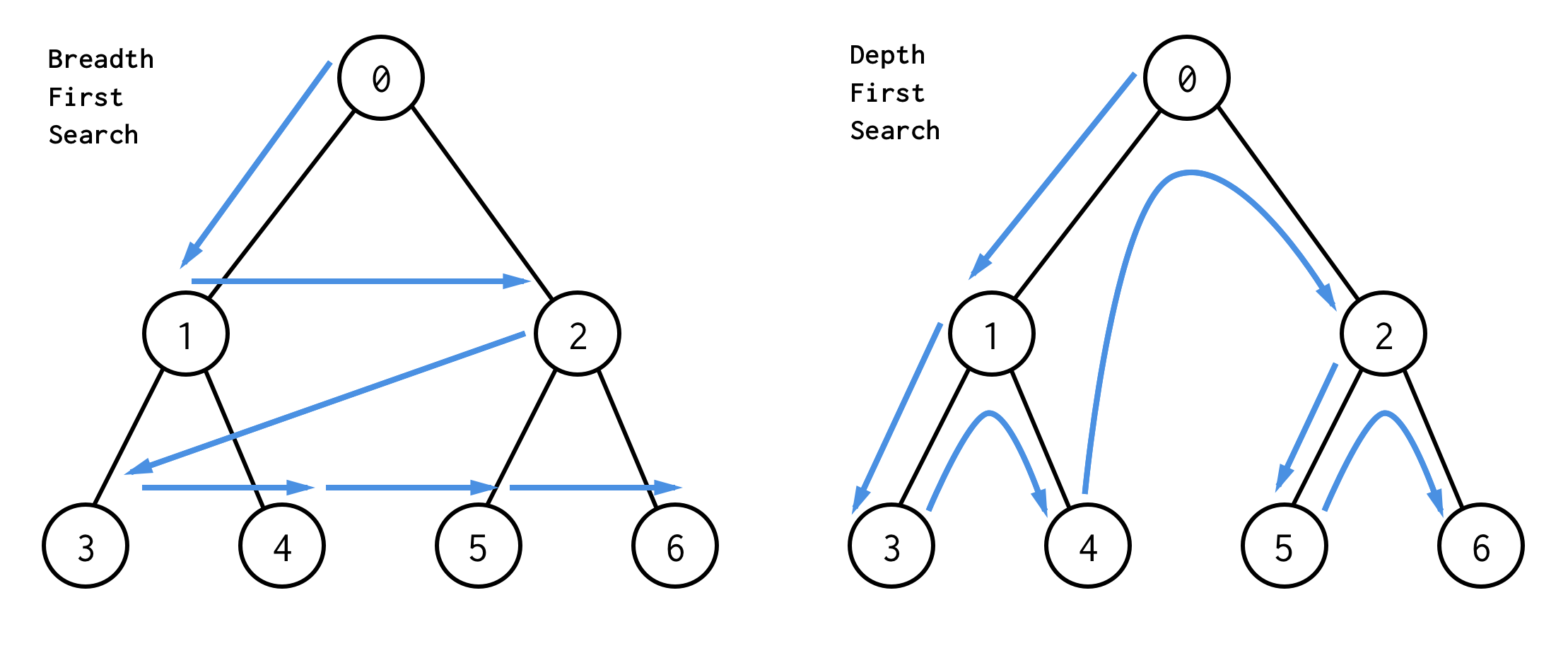
As indicated in the figure, there are different ways to "walk" a tree. Plans walks the tree in a depth first fashion, which is something we'll get back to.

Each node in the tree (numbered bubbles) plays one out of three possible roles, acting either as a plan, a rule, or a stop.

These are just names we invented, but together they allow us to string together algebraic expressions of the form:

((a + b) + f(c + d + e))

The mathematical terms in this expression, a, b, c, d and e, correspond to stops.

The parentheses in the expressions correspond to plans, which allow you to create super-terms out of yet another expression.

The function call f(...) corresponds to a rule being applied to the plan (c + d + e), which will modify the output of that plan.

Algebra?

The tree is just another way to represent what we just spelled out, simple algebraic expressions.

Let's look at a concrete case, and note how the tree is "walked" in Plans:

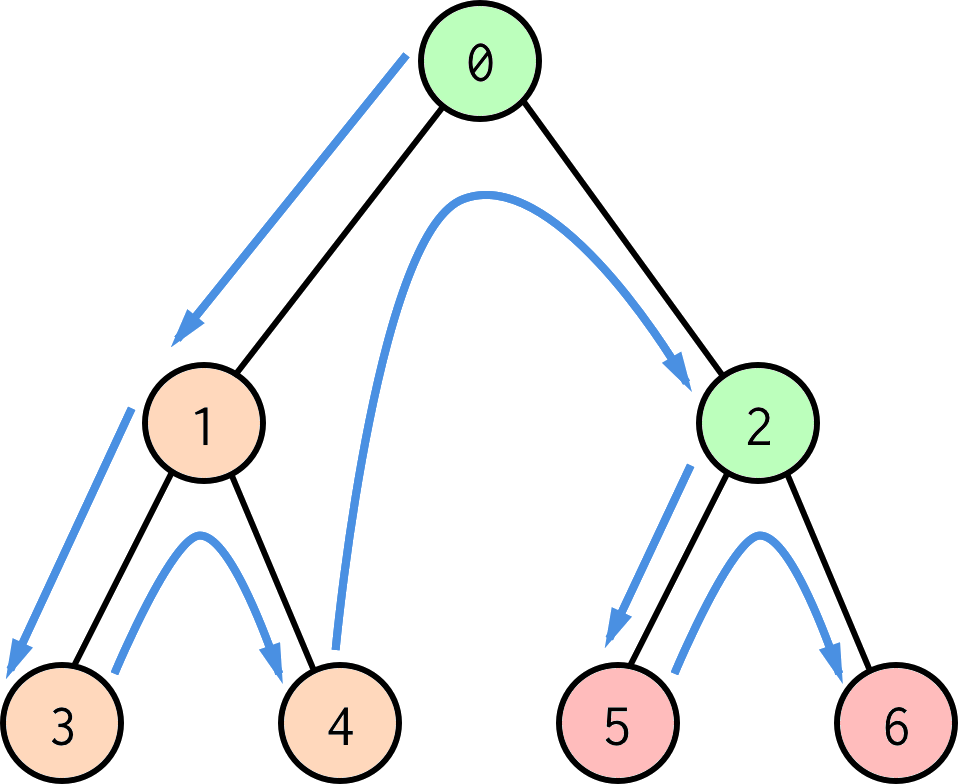
Here we have color coded green as plans, orange as rules, and red as stops.

1. We start at the top, #0, which is always a plan - here we get the outer parentheses ()
2. We get to #1, which is a parent rule - here we are just remembering that "#1" exists within this scope
3. We get to rules #3 and #4 - again we are just remembering "#3" and "#4" for later
4. Now we get to plan #2, and let's say plan #2 mentions rule #4 - now we have built ourselves up to the expression (rule4(...))
5. Finally we encouter the two stops #5 and #6 - this leaves us with a complete expression (rule4(term5 + term6))

And the tree can go on like this, in general allowing us to build nested expressions that look like this:

(someFunction(variable + anotherFunction(anotherVariable + ...)) + outerFunction(innerFunction(yetAnotherVariable + ...)) + ...)

But there's more. Next, we take a look at the inside of the bubbles.

Plans

As mentioned before, plan bubbles allow us to create parentheses, a term consisting of other terms. These bubbles can contain any other type of bubbles. They also allow us to refer to rules that have been discovered previously on the walk. One thing to note here is that when we pop out of a plan in the walk, the rules inside it are forgotten. This allows us to control the scopes of various formulas we want to use in our tree.

Finally, plan bubbles have a couple of other features we won't dive into here, mainly dealing with multiple units flowing through the same expressions, a concept called "branching", as well as ways to scale your results without the use of custom functions.

Rules

Rule bubbles represent custom, user-defined functions. They can only contain other rule bubbles. They may contain calculations of the sort [Duration] = [Distance] / [Speed], or they could just call upon calculations defined by previously discovered rule bubbles; or they may mix and match their own calculations with such other calculations.

The variables in the calculation is often input from a plan, as we've teased before. Another feature of rules is that they can define their own constants/variables to be used when none are given from the plan that calls upon them.

Stops

When we reach stop bubbles, we start completing our master expression with inner terms, and begin seeing actual numbers flowing through the nested expressions. Stops don't contain anything else.

These terms can be just thought of as singular numbers, but in Plans they are typically ~10k element vectors sampled from various distributions. The algebra stays the same.